The sliding window algorithm is a technique used in computer science for solving problems involving arrays, strings, or other linear data structures. It involves moving a window (a subarray or substring) of a fixed size through the given data structure and performing some operation on the elements within the window.

How do we know whether to go for SWA?

(SWA) - Sliding Window Algorithm

1) If the problem involves processing a fixed-size window of elements at a time, or if the problem statement explicitly mentions finding patterns, substrings, or subsequences within the data structure, sliding window might be a suitable approach.

2) Data Structure: Sliding window is commonly used with linear data structures such as arrays or strings. If the problem involves such data structures and requires examining contiguous elements or substrings, sliding window could be a good fit.

Let's have a look into the Algorithm then talk where we can implement them How>Where>When

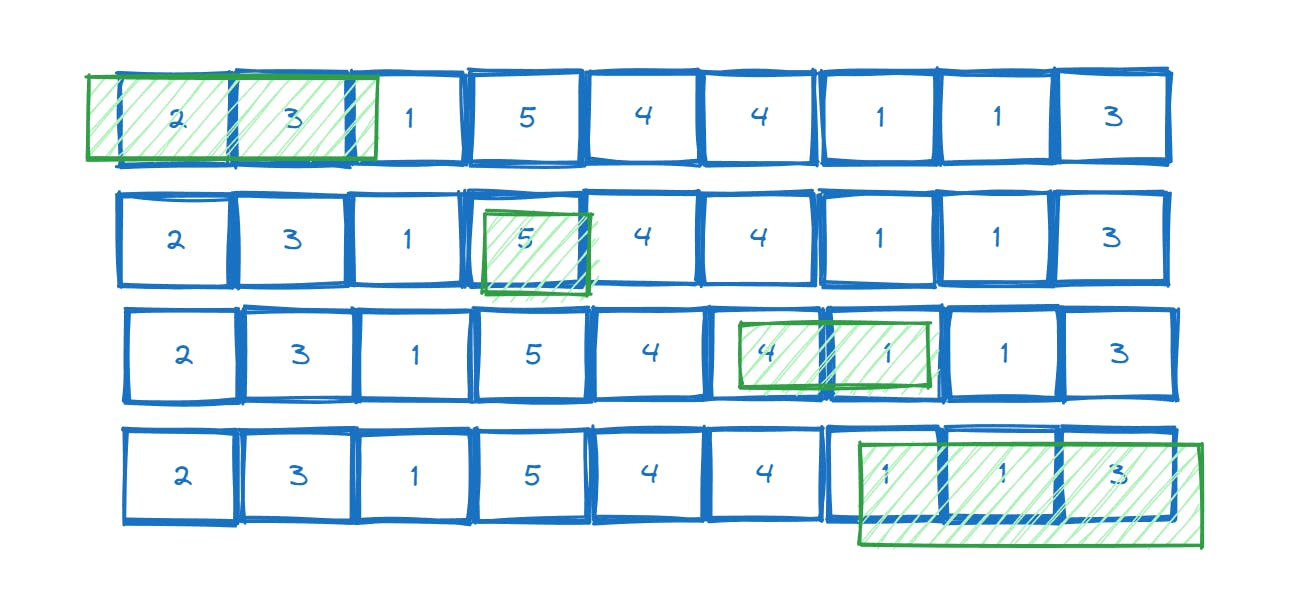
Find a contiguous subarray of length 3 having sum 5

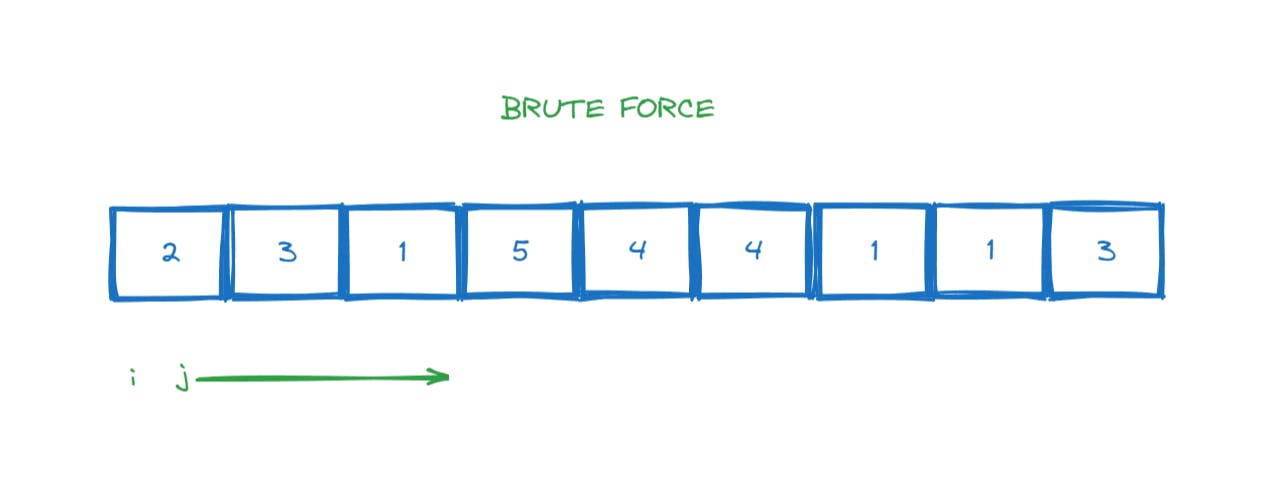
When we apply double or triple for loop we can definelty solve this problem too but the time complexity goes >>>>> O(n^2) and O(n^3)

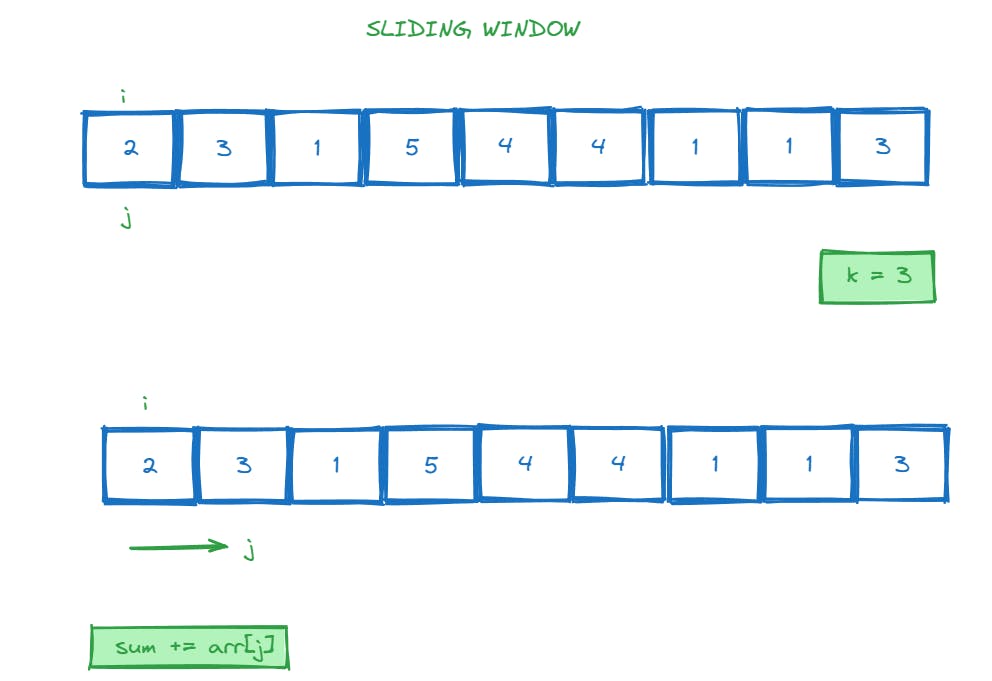
Let's go with Two Pointers initialized from i = 0; j = 0;

 //initializing two pointers
        int i = 0;
        int j = 0;

 windowSum += nums[j];
            j++;

Let's sum up according to the question

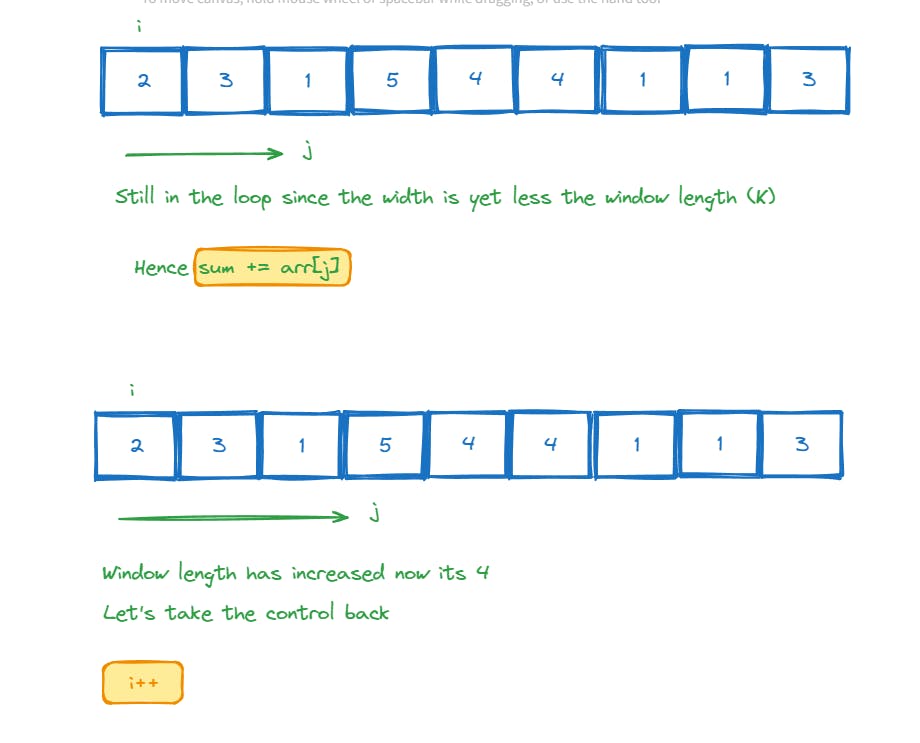
 //Make the window small if the k increases i.e i++ and j++
            if(j - i > k){
                windowSum -= nums[i];
                i++;
            }

            //Update the maximum sum
            if(j - i == k){
                maxSum = Math.max(maxSum, windowSum);
            }

Final Code

package Intermediate;

public class SlidingWindow {

    public static int maxSum(int[] nums, int k){
        if(nums == null || nums.length == 0 || k <= 0 || k > nums.length){
            return 0;
        }

        int maxSum = Integer.MIN_VALUE;
        int windowSum = 0;

        //initializing two pointers
        int i = 0;
        int j = 0;

        //Actual implementation of sliding window
        while (j < nums.length) {
            windowSum += nums[j];
            j++;

            //Make the window small if the k increases i.e i++ and j++
            if(j - i > k){
                windowSum -= nums[i];
                i++;
            }

            //Update the maximum sum
            if(j - i == k){
                maxSum = Math.max(maxSum, windowSum);
            }
        }

        return maxSum;
    }

    public static void main(String[] args) {
        int[] nums = {1, 3, -1, -3, 5, 3, 6, 7};
        int k = 3;
        int result = maxSum(nums, k);
        System.out.println("Maximum sum of subarray of size " + k + ": " + result);
    }
}

LeetCode

239 - leetcode.com/problems/sliding-window-maximu..

2653 - https://leetcode.com/problems/sliding-subarray-beauty/description/

413 - https://leetcode.com/problems/arithmetic-slices/description/